I. Introduction▲
La construction de labyrinthes parfaits est soumise à deux conditions fondamentales :
- Il doit toujours exister un chemin entre deux points du labyrinthe (connexité).
- Il existe au plus un chemin entre deux points d'un labyrinthe (acyclicité).
De multiples algorithmes permettent d'obtenir de bons résultats, Prim, Kruskal, Aldous-Broder, Wilson, Euler, … J'ai posé mon choix sur une variante de l'algorithme de Kruskal. De plus, au-delà de la mise en place de l'algorithme, il m'a semblé intéressant d'employer les ensembles de Tarjan. Cette solution ne m'est pas exclusive m'avait fortement inspiré il y a quelques années. L'idée peut paraître fantaisiste ou compliquée, cependant elle tend à donner une solution originale compte tenu du sujet de l'article.
| Algorithme | Impasse en % | Type | Technique | Hétérogénéité | Bufferisation mémoire | Temps | Solution en % |
|---|---|---|---|---|---|---|---|
| Backtracker récursif | 10 | Arbre | Passage | Oui | Oui | 24 | 19.0 |
| Hunt and Kill | 11 | Arbre | Passage | Non | Non | 55 | 9.5 |
| Arbre binaire | 25 | Ensemble | Tous | Non | Non | 7 | 2.0 |
| Eller | 28 | Ensemble | Tous | Non | Non | 10 | 4.2 |
| Wilson | 29 | Arbre | Tous | Oui | Oui | 51 | 4.5 |
| Aldous-Broder | 29 | Arbre | Tous | Oui | Non | 222 | 4.5 |
| Kruskal | 30 | Ensemble | Tous | Oui | Oui | 32 | 4.1 |
| Prim | 36 | Arbre | Tous | Oui | Oui | 21 | 2.3 |
| Arbre à croissance rapide | 49 | Arbre | Tous | Oui | Oui | 43 | 11.0 |
- La colonne impasse indique le pourcentage approximatif de cellules sans avenir dans le labyrinthe.
- Il y a deux types d'algorithmes de création de labyrinthe : le premier basé sur un arbre grossissant et le second sur un ensemble.
- La plupart des algorithmes peuvent être mis en application en découpant des passages ou en ajoutant des murs mais certains sont restreints à une seule des deux techniques.
- L'hétérogénéité indique si un algorithme traite toutes les directions et côtés du labyrinthe également, sans polarisation.
- La bufferisation mémoire indique si aucune mémoire ou pile supplémentaire n'est exigée pour mettre en place l'algorithme.
- Le temps donne une idée sur la durée nécessaire à l'application de l'algorithme.
- La solution indique le pourcentage de cellules que le chemin de réussite doit traverser.(cf. Maze Classification, Walter D. Pullen)
II. Au départ…▲
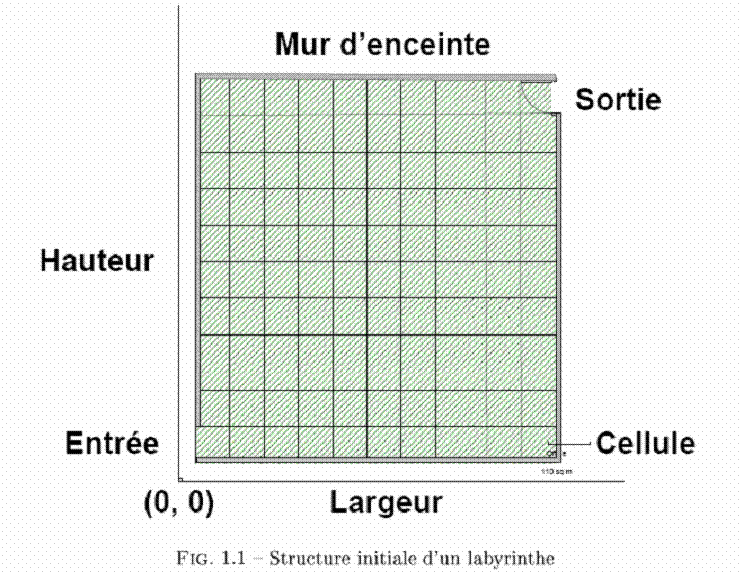
Un labyrinthe rectangulaire parfait est représenté par une classe qui accepte le nombre de lignes et de colonnes. On appellera largeur et hauteur respectivement le nombre de lignes et de colonnes de ce labyrinthe. Ainsi, cette classe alloue un tableau de type largeur*hauteur=nombre de cellules dont deux cellules voisines sont toujours séparées par une porte, celle-ci pouvant être ouverte (permettant le passage), fermée ou fermée à clé. Parmi ces dernières, nous devons distinguer les portes verticales et les portes horizontales. Enfin, une enceinte comprenant une ouverture à chaque extrémité entoure le labyrinthe.
À cet effet, nous dessinons deux classes, Cellule et Labyrinthe ayant les signatures suivantes (Notation ASN.1, i.e. ASN.1 Information Site) :
Cellule ::- {
ensemble ::- Entier
etat ::- Entier
identificateur ::- Entier
}Labyrinthe ::- {
largeur ::- Entier
hauteur ::- Entier
cellule ::- Cellule[]
}Télécharger les classes Labyrinthe.java et Cellule.java.
Les données principales de chaque cellule sont codées sur trois entiers. Le premier spécifie l'ensemble auquel elle appartient, le deuxième l'état de ses portes et enfin, le dernier est un identifiant unique (ID). Toutes les cellules possèdent quatre portes (Nord, Est, Sud et Ouest) qu'elles partagent (sauf aux bords) avec une cellule voisine. Ainsi, nous considérons que chaque cellule, à l'exception des bords, ne gère que deux portes (Sud et Est i.e. le repère possède une origine en bas à gauche). Nous représentons alors l'état des portes par deux bits avec la convention suivante :
00 ::- La porte est fermée
01 ::- La porte est ouverte
02 ::- La porte est fermée à cléPar ailleurs, nous décidons de coder l'état sur 4 bits, les deux premiers étant liés à la porte Sud et les deux suivants à la porte Est en considérant une écriture big-endian.
L'Endianisme est la manière de ranger les octets en mémoire : on distingue ainsi les little-endian (octet de poids faible en tête) et les big-endian (octet de poids fort en tête).
| Valeur décimale | Valeur binaire | Est | Sud |
|---|---|---|---|
| 0 | 00 00 | Fermée | Fermée |
| 1 | 00 01 | Fermée | Ouverte |
| 3 | 00 11 | Fermée | Fermée à clé |
| 4 | 01 00 | Ouverte | Fermée |
| 5 | 01 01 | Ouverte | Ouverte |
| 7 | 01 11 | Ouverte | Fermée à clé |
| 12 | 11 00 | Fermée à clé | Fermée |
| 13 | 11 01 | Fermée à clé | Ouverte |
| 15 | 11 11 | Fermée à clé | Fermée à clé |
III. Les ensembles de Tarjan▲
Lors de l'ouverture des portes du labyrinthe, il est souvent nécessaire de savoir si deux cellules données sont déjà reliées entre elles ou non. Il est donc important de trouver une technique permettant d'effectuer cela de manière efficace. Une idée qui vient rapidement à l'esprit est de former des ensembles de cellules pour savoir lesquelles sont connectées entre elles. Les deux opérations que vont devoir effectuer ces deux ensembles sont la COMPARAISON et l'UNION de deux ensembles. À cet effet, l'utilisation des Ensembles de Tarjan est une approche reconnue. Nous désignons ainsi pour chaque ensemble un élément représentatif. Comparer deux ensembles revient alors à tester si leurs représentants sont identiques, tandis que mettre en commun deux ensembles revient à élire un nouveau représentant commun à ces deux ensembles.
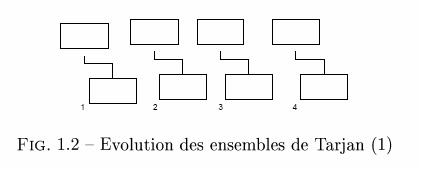
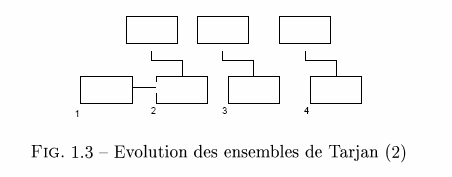
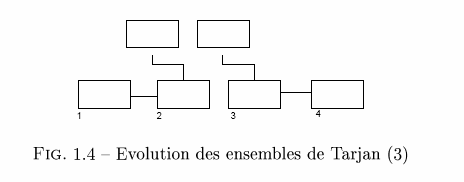
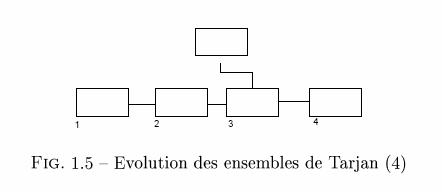
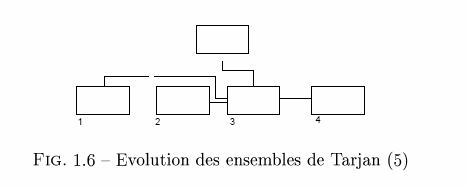
La création d'un Ensemble de Tarjan met en place une classe Tarjan contenant à la fois une cellule représentative de l'ensemble et un ensemble de cellules (Notation ASN.1) :
Tarjan ::- {
representant ::- Cellule
ensemble ::- java.util.Vector
}Cette classe fournit de plus deux méthodes :
Elles permettent respectivement de tester si une cellule appartient au même ensemble qu'une autre et de mettre en commun deux ensembles. Nous pouvons remarquer qu'une mise à jour de l'ensemble des cellules d'un ensemble A_2 est nécessaire lors de l'union avec un ensemble A_1 dont le représentant devient celui du nouvel ensemble : A = A_1 U A_2.
Télécharger la classe Tarjan.java.
IV. L'algorithme de Kruskal▲
Rappelons-le, l'unique contrainte pour que le générateur réalise un véritable labyrinthe est l'existence d'un chemin unique entre chaque pièce du labyrinthe. L'algorithme employé doit donc être divisé comme suit :
- Génération de tous les murs.
- Destruction de certains murs afin de former le labyrinthe.
D'un point de vue technique, il s'agit de représenter l'ensemble des trajectoires possibles par un arbre de recouvrement. D'un point de vue pratique, la règle consiste à ne pas ouvrir une porte entre deux cellules si celles-ci peuvent déjà se rejoindre par un autre chemin. Ainsi, la destruction des murs doit se faire en deux étapes récurrentes :
- Tester si deux murs appartiennent à la même classe d'équivalence.
- Unir deux classes d'équivalence.
En procédant de cette manière, nous nous assurons du respect des conditions de connexité et d'acyclicité. Un problème majeur est cependant posé par le parcours aléatoire des cellules. Le choix s'est posé sur un mélange préalable de la totalité de l'ensemble permettant de ne plus avoir à s'en soucier par la suite.
DEPART
Marquer chaque cellule de manière unique avec un identificateur
TANT QUE le labyrinthe n'est pas fini,
FAIRE se placer au hasard sur une cellule non parcourue.
SI on trouve une porte fermée,
ALORS regarder l'identificateur de la cellule voisine.
SI les identificateurs sont différents,
ALORS ouvrir la porte commune et unifier leurs identificateurs ainsi que leurs listes
SINON fermer la porte à clé.
FIN TANT QUE
FINAu niveau de la programmation, nous mettons en place la classe suivante, dont le constructeur se charge d'initialiser les différentes variables et de mélanger le Vertex (l'ensemble des sommets du graphe i.e. l'ensemble des cellules du labyrinthe).
Kruskal ::- {
labyrinthe ::- Labyrinthe
vertex ::- java.util.Vector
tarjan ::- java.util.Vector
hasard ::- java.lang.Random
}Télécharger la classe Kruskal.java.

V. Sim labyrinthes Intellgo▲
Intellego est un outil réalisé par Graham Ritchie permettant d' expérimenter des techniques robotiques. Il fournit un cadre de travail pour le développement de programmes de contrôle de robots Lego RCX en Java. Intellego permet également de développer des univers de simulation divers dans lesquels évolueront des robots.
Intellego permet de concevoir de nouveaux mondes appelés SimWorld, il suffit simplement de créer une classe héritant de BasicSimWorld. Nous pouvons ensuite disposer différents objets à l'intérieur :
- Les murs SimWall.
- Les sources de lumière SimLight.
- Les robots SimRCX.
Dans notre cas, les labyrinthes conçus par l'algorithme de Kruskal seront représentés par des SimWorlds ne comportant uniquement que des SimWalls dans lequel évolueront des SimRCXs. Nous implémentons alors une classe SimLabyrinthe dont le constructeur fait appel à un labyrinthe généré par l'algorithme de Kruskal. Cette classe traite les informations reçues pour bâtir un SimWorld.
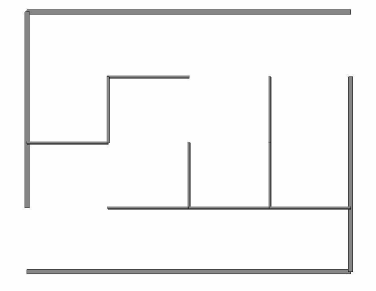
Bien entendu, la technique employée pour bâtir les labyrinthes permet de gérer des labyrinthes plus complexes, c'est l'affichage qui marque la différence.
- Télécharger la classe SimLabyrinthe.java.
- Télécharger Intellego.
VI. Remerciements▲
Je tiens à remercier l'ensemble de l'équipe de Développez.com et plus particulièrement jab et greg01 pour leur relecture.